Kotlin refactoring: 8 tips from practice

Introduction

A great feature of exercism is that once you complete an exercise, you can compare your solution with the ones other practitioners have written. This piqued my curiosity, so after I completed a few Kotlin exercises as part of the #12in#23 initiative, I went on to see how I could refactor my code to make it more idiomatic.

The following overview is what came out of that: each section corresponds to one exercise. I’ll give you a brief intro to the task, then show you my solution and finally share some refactoring tips I enjoyed.

If you recently started coding in Kotlin or if you’d like to get a sense for some of the language features in action, then you might find this helpful and discover some compelling use cases.

Just count…

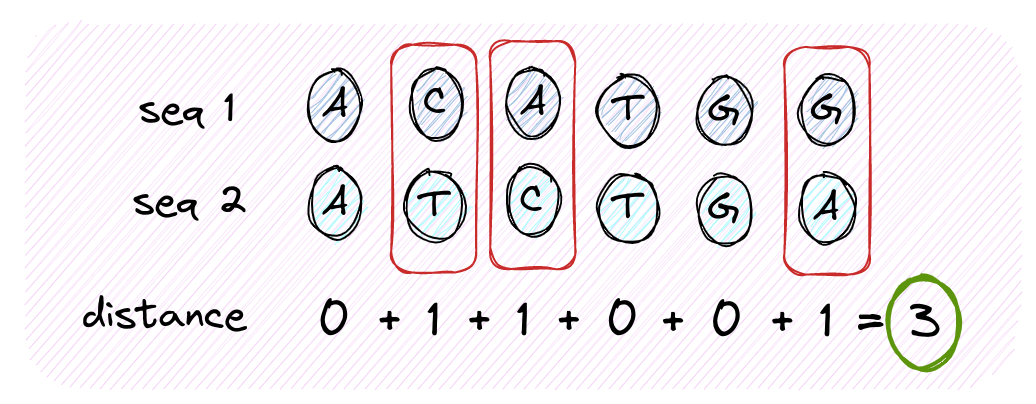
Figure 1. Two DNA sequences are represented: A C A T G G and A T C T G A. The distance between the two is computed as the sum of occurrences where two distinct bases appear in the same position. In this case: distance = 0 + 1 + 1 + 0 + 0 + 1 = 3 — Figure 1. Counting the number of differences (*distance*) between two DNA sequences.

In the first exercise, I was tasked to count differences across two DNA sequences - which is analogous to comparing two arrays for equality element-wise. My approach was to zip the two and fold.

fun compute(leftStrand: String, rightStrand: String): Int {
  if (leftStrand.length != rightStrand.length) {
    throw IllegalArgumentException(
      "left and right strands must be of equal length")
  } 
  return leftStrand.split("")
    .zip(rightStrand.split(""))
    .fold(0) {
        count, (l,r) -> count + (if (l == r) {0} else {1})
    }
}

I found 3 improvements based on other solutions:

there is no need to .split the strings before zipping them. This is because String implements the CharSequence interface, which includes an implementation of .zip.
fold is always fun to use, but Kotlin offers a better alternative when the goal is to count instances satisfying a predicate: Array#count accepts a predicate and returns the number of instances where the predicate evaluates to true. This is just what we were looking for!
When it comes to making assertions on the parameters of a function, Kotlin offers the idiomatic require, which raises an IllegalArgumentException when the value passed is false.

fun compute(leftStrand: String, rightStrand: String): Int {
  require(leftStrand.length == rightStrand.length) {
    "left and right strands must be of equal length"
  }

  return leftStrand
    .zip(rightStrand)
    .count { it.first != it.second }
}

Closer look. Note how convenient it is to be able to use the implicit name it for the lambda passed to count. This works anytime you have a lambda with a single argument.

Constructor once, constructor twice

An exercise required to define a class with two 1-argument constructors accepting different types. My instinct was to define two constructors explicitly, so I wrote the following.

// Given a date/time, this class computes what the `LocalDateTime` 10^9 seconds in the future will be.
class Gigasecond {
  val gigaSeconds = 1e9.toLong()

  val date: LocalDateTime
  constructor(initialDate: LocalDateTime) {
    date = initialDate.plusSeconds(gigaSeconds)
  }

  constructor(initialDate: LocalDate) : this(initialDate.atStartOfDay())
}

It turns out there is a more idiomatic option: we can use Kotlin primary constructor to save some code and remove any ambiguity around where and how the field date is initialised.

class Gigasecond(initialDate: LocalDateTime) {
  val gigaSeconds = 1e9.toLong()

  val date = initialDate.plusSeconds(gigaSeconds)

  constructor(initialDate: LocalDate) : this(initialDate.atStartOfDay())
}

Fun fact: while looking at the community solutions, I got reminded of the exponential notation as a shorthand to define large Double numbers. My first take in defining the gigaSecond constant was the unnecessarily convoluted (10.0).pow(9).toLong(), which among other things requires importing kotlin.math.pow 😅 Anyway, read on for some more pow fun.

Closer look. Note that I didn’t discuss the topic of class constants in this section. If you are interested, companion objects are worth a look, although some shortcomings apply.

Circling around squaring

An exercise asked to compute the square of the sum of the first n natural number. It turns out there is a formula for that: (n(n + 1) / 2)², so I wrote

fun squareOfSum(n: Int): Int {
  return (n * (n + 1) / 2).toDouble().pow(2).toInt()
}

I found two improvements:

Note how we go toDouble in order to invoke Double#pow, then have to convert back to Int with toInt. Instead, we could simply multiply the base by itself - this is a classic and recurring optimisation in code dealing with numerical computing. In other languages, we’d have to define x = n * (n + 1) / 2, then return x * x. In Kotlin, we can use let, which passes the receiver object as argument to a lambda and returns the result of the lambda.
A nice shorthand applies when a function’s body is a single expression. From the docs: “When a function returns a single expression, the curly braces can be omitted”. In that case, the body is specified after the = sign.

fun squareOfSum(n: Int): Int = (n * (n + 1) / 2).let { it * it }

Mutatis mutandis

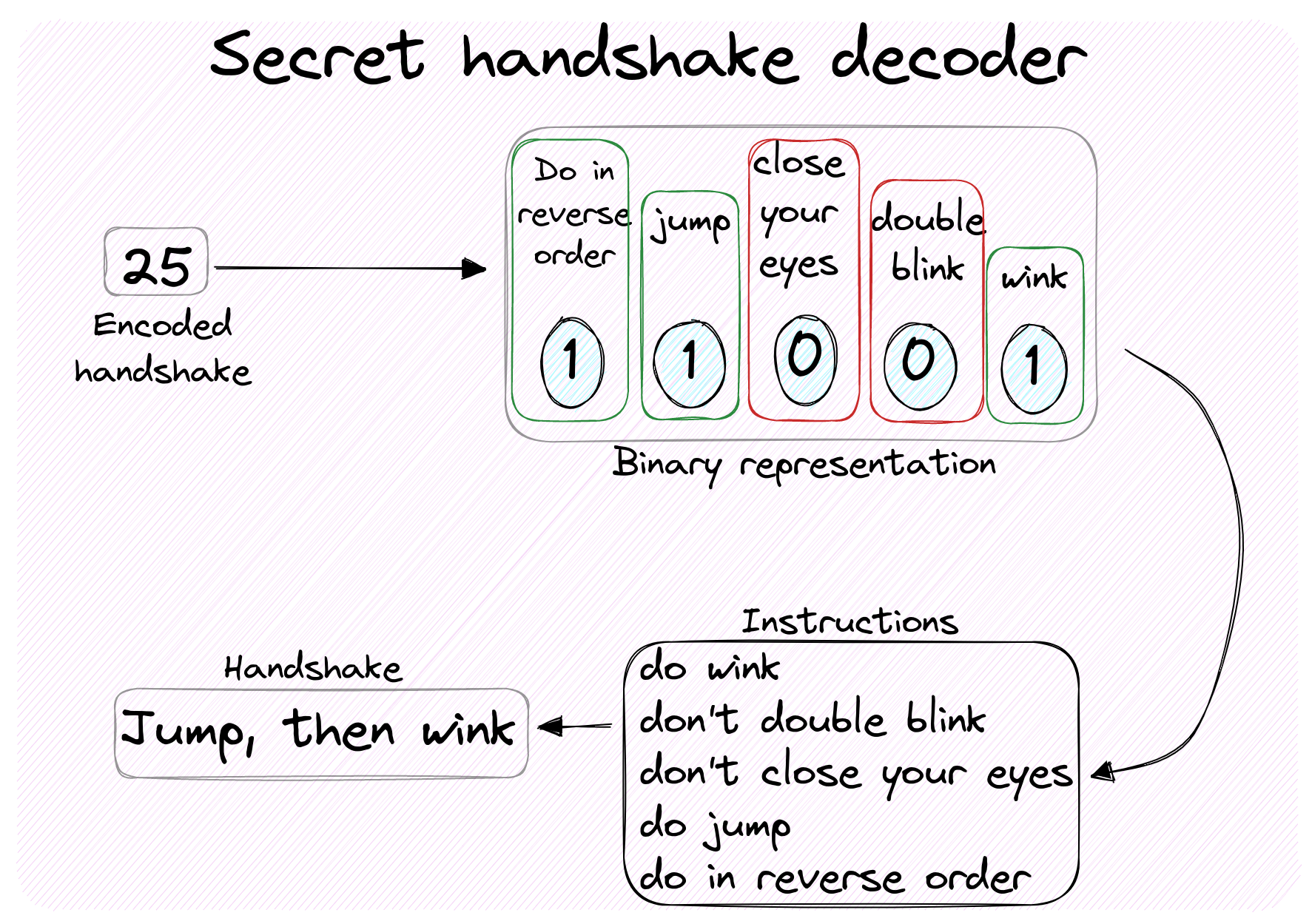
Figure 2. The integer 25 is transformed to its binary representation: 1 1 0 0 1. From the right, the first 4 bits represents a signal: wink, double blink, close your eyes, jump. When a bit is 1, it is part of the handshake sequence. The fifth bit acts as a modifier: when it's 1, it reverses the sequence of signals. The handshake represented by the numbre 25 is Jump, then wink. — Figure 2. Decoding an integer into a sequence of signals making up a secret handshake based on its binary representation.

The next exercise asked to decipher the binary representation of an integer into a sequence of signals for a secret handshake. I came up with the following code.

object HandshakeCalculator {
  val reverseList = 0b10000

  fun calculateHandshake(number: Int): List<Signal> {
    var lst = mutableListOf<Signal>()
    Signal.values().forEach {
      if (number.and(it.int) == it.int) { lst.add(lst.size, it) }
    }
    if (number.and(reverseList) == reverseList) { 
      return lst.reversed()
    } else {
      return lst
    }
  }
}

I really like that we can iterate over the values of the Signal enum with Signal.values().forEach, but I thought the way we alter the signal sequence lst could be improved. In fact, turns out we can do without declaring that variable altogether:

We can modify the initial MutableList with an apply block, which lets us succintly call side-effecting methods on the receiver (A.K.A. the context object) and then returns it.
We can extract the code for checking whether a bit appears in a number into its own function. As a bonus, we can even make that an extension function on the type Int 😎

object HandshakeCalculator {
  val reverseList = 0b10000

  fun calculateHandshake(number: Int): List<Signal> =
    mutableListOf<Signal>().apply {
      Signal.values().forEach {
        if (number.boolAnd(it.int)) add(size, it)
      }
      if (number.boolAnd(reverseList)) reverse()
    }
  
  private fun Int.boolAnd(bit: Int): Boolean = and(bit) == bit
}

EDIT: a fellow redditor suggested that a nicer way to build the list is to use buildList in place of mutableListOf<Signal>().apply. This lets us abstract away from a specific list implementation and omit the generic type, which is inferred based on the add operations.

Closer look. If you come from other languages where adding functionality to classes outside our control is frowned upon, then the concept of extension functions might feel like a code smell to you. I think Kotlin’s implementation of this functionality is quite different than you might expect though: as specified in the docs, “Extensions do not actually modify the classes they extend. By defining an extension, you are not inserting new members into a class, only making new functions callable with the dot-notation on variables of this type”. Also, mind that the private keyword acts as a visibility modifier that ensures no one outside of the scope where the extension is defined can access that.

Closer look. Note how we moved from reversed to reverse. The first returns a new MutableList, the latter modifies the list in-place and is more suited for the apply approach - once you’re mutating objects, you might as well embrace mutability! As a general tip, to determine whether a method / function is mutating the caller / target, pay attention to the returned type in the signature. When Unit is returned, you’re likely looking at side-effecting code.

Challenge. Can you rewrite calculateHandshake to operate on immutable collections only? :light_bulb: Hint: you could consider filtering through signals.

lbarasti's blog